Новый метод неотрицательного байесовского суммирования для прогнозирования выживаемости при раке с использованием многомерных данных омики. Методология медицинских исследований BMC

Стратегия выживания на основе пути

Предположим, что данные о выживании подвергаются цензуре справа. н Темы состоят из троек {(й_я, δ_я,с_я)},л я= 1, 2, …, н. Указывает наблюдаемое время выживанияй_я= минута( р_я, С_я), где р_я ИС_я — время события и время цензурирования соответственно. δ_я«=» я ( р_я<С_я) указывает на возникновение событий. Цель состоит в том, чтобы оценить функцию выживания случайной величины времени события.Да Это зависит сКовариаты слюбой с( й|с«=» с(Да > й |с). В этом исследовании мы стремимся предсказать выживаемость больных раком, используя геномные данные.

Предлагаемый метод суммирования выживания представляет собой двухуровневую архитектуру обучения, состоящую из нескольких базовых обучающихся (подмоделей) и отдельного обучающегося (метамодели). См. рисунок 1 для потока кадров.

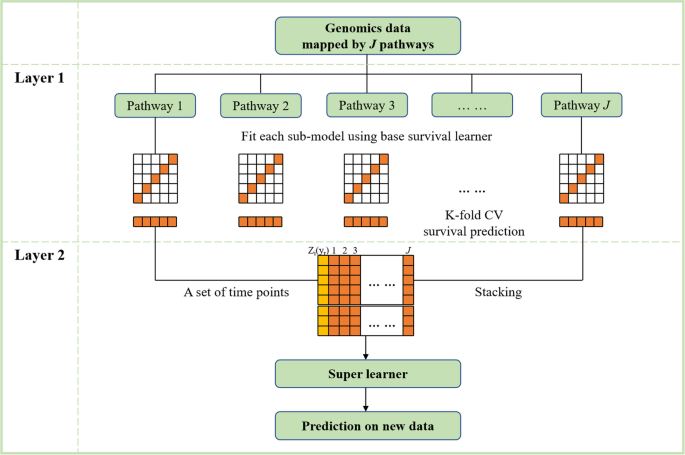
Алгоритмическая схема предлагаемой модели суммирования выживания. Резюме: проверено

Сначала мы преобразуем данные генома вССубданные, содержащие гены каждого пути. Затем на первом уровне подмодели обучаются независимо для каждого подданных. Полученные подмодели отражают предсказательную силу траекторий. Чтобы смягчить переобучение, мы рассчитываем перекрестно проверенные предикторы выживаемости на основе подмоделей. В частности, при каждом проходе исходные выборки данных случайным образом разбиваются. КПодгруппы (складки) одинакового (грубого) размера. тот К^й Сгиб используется в качестве данных проверки, Пятый(К), а остальные складки — обучающие данные,Т(-К),К= 1, 2, …, К . В обучающих данных можно использовать модель штрафа Кокса, чтобы соответствовать подмодели и основным рискам.ЧАС₀^{— К}( й^—К) можно оценить по методу Бреслоу. Тогда линейный предиктор (лп^К) в данных проверки оцениваются подобранной подмоделью. Предполагаемые вероятности выживания \({\hat {S}}^k\left({y}^k|\boldsymbol{x}\right)\) вПятый ( К ) можно рассчитать с помощьюлп^К ИЧАС₀^—К( й^{— К}), это

где \({H}^{-k}\left({y}^{-k}\right)={H}_0^{-k}\left({y}^{-k}\right)\times {e}^{l^k}\), \({H}_0^{-k}\left({y}^{-k}\right)\) Это совокупный базовый риск, т.е. неотъемлемая часть ЧАС₀^{— К}( й^{— К}). Процесс повторяется для всех К складки, что дает прогнозируемые вероятности выживания CV для всех случаев. к С Подмодели, которые мы можем получить С Прогнозы \({{\hat{S}}_j}^{CV}\left(y|\boldsymbol{x}\right)=\sum_{k=1}^K{{\hat{S}}_j}^ k\left({y}^k|\boldsymbol {x}\right),\kern0.5em j=1,2,\dots, J\). Второй уровень использует отдельного обучающегося, чтобы соответствовать ожиданиям выживания CV. С Подмодели по набору моментов времени. Полученные коэффициенты представляют собой расчетные веса \({\hat{w}}_j\) кСПодмодели. Функция прогнозирования выживания \(\hat {S}\left(y|\boldsymbol {x}\right)\) Его можно оценить путем объединения предикторов СПодмодели \({\hat{S}}_j\left(y|\boldsymbol{x}\right)\) (Обновить исходные данные) с использованием весов \({\hat{w}}_j\).

Метод оценки весов \({\hat{w}}_j\)

Линейный комбинированный подход

Обычно функция выживания является прогнозирующей. \(\hat {S}\left(y|\boldsymbol {x}\right)\) Это линейная комбинация предикторов С Подмодели-кандидаты задаются как:

Улучшаем веса \(\шляпа{ш}\) За счет уменьшения потери синдрома раздраженного кишечника. Другая функция потерь, такая как потеря на основе AUC, должна быть подходящей альтернативой. [22]. IBS измеряет квадрат расстояния между вероятностями и наблюдаемыми событиями в течение набора моментов времени.й₁,…,й_с [23]что можно записать как,

где р( й_с) представляет пациентов, которые на данный момент все еще находятся в группе риска й_с, г_я(й_с«=» я( й_я> й_с). Мы можем оценить \(\шляпа{ш}\) За счет снижения частоты синдрома раздраженного кишечника. Общий расчетный вес \({\hat{w}}_j\) Ограничено неотрицательностью для меньшей дисперсии и лучшего прогнозирования. Этого ограничения можно достичь с помощью алгоритма нелинейной оптимизации, основанного на расширенном методе Лагранжа, который можно реализовать в функции R. сольп [24]. По поводу выбора временных блоков й₁,…, й_смы используем девять равноотстоящих друг от друга величин для распределения наблюдаемых событий, как это назвал Эндрю Уэй. [19].

Байесовский комбинированный подход

В дополнение к решениям IBS, если мы будем рассматривать предикторы выживания подмодели как ковариаты и рассматривать случай, зависящий от времени г_я( й_с(0) для мертвых и 1 для живых в каждый момент времени й_с) В качестве бинарного результата ожидаемая выживаемость может быть выражена как:

Это обобщенная линейная модель (GLM).ЧАС Это корреляционная функция, такая как сигмовидная функция, гарантирующая, что ожидаемая вероятность выживания равна 0–1.

Неотрицательное лассо (nLasso)

Прогрессия формулы (4) заключается в том, что мы можем добавить к 1 штрафной член в приведенном выше GLM, что расширяет использование суммирования выживания, например, для работы со многими подмоделями (в многомерном сценарии), что непрактично для solnp.

Известно, что Лассо эквивалентно байесовской иерархической модели с DE, предшествующим коэффициентам [25]с коэффициентами, квалифицируемыми в этом исследовании как неотрицательные,

Где масштаб,с Контролирует степень усадки. Меньший размер приводит к более сильному сокращению, что приводит к занижению оценок. че_Да К нулю. Веса, оснащенные nLasso, определяются следующим образом:

Вышеупомянутые веса можно оценить с помощью алгоритма отношения периодических координат, используя ком. Пакет в Р. ограничениече Быть непассивным можно легко, используя ком. выселение.

Неотрицательное лассо шипа и плиты (nsslasso)

Мы также расширяем неотрицательный DE до неотрицательного возвышения и смесь плит до DE (дополнительный рисунок 1),

где с_Да= (1 — γ_Да) с₀ + γ_Дас₁ Он называется параметром общего диапазона. γ_Да это указатель ( γ_Да €{0, 1}) после биномиального распределения; с₀ И с₁ ( с₁ >с₀ > 0) — масштабные параметры распределения высоты и плиты соответственно.с₁ Он применяет более слабое сжатие к более сильным путям эффектов и обычно имеет большее значение, напримерс₁ = 1; пока с₀Он обеспечивает более сильное сжатие для путей слабого влияния (или даже сжатие до нуля) и представляет собой гибкое меньшее значение, выбранное из набора значений-кандидатов, заранее определенных посредством перекрестной проверки. Лассо с шипами и плитами обычно более адаптируемо, чем лассо. [26]. Веса можно оценить с помощью алгоритма соотношения координат EM. [26] с использованиемком.пакет иБахджалам пакет в R. Ограничение неотрицательности весов также можно выполнить с помощьюком.выселение.

Искусственная нейронная сеть

Учитывая, что ИНС может действовать как классификатор и придавать входным данным ограниченный (неотрицательный) вес, мы можем использовать ее в качестве дискриминантного обучающегося. ИНС использует алгоритм обратного распространения ошибки и алгоритм градиентного спуска для итеративной оценки весов.

Оцените производительность модели

В принципе, модель суммирования выживаемости представляет собой задачу бинарной классификации за заданный период. [21]. Здесь мы использовали зависящую от времени AUC и зависящую от времени оценку Бриера (BS), которая рассчитывает AUC и BS для организмов в группе риска в любой момент времени, как рекомендовал Роберт Тибширани. [21]. Зависящая от времени AUC используется для проверки способности модели различать различные результаты в данный момент времени. Зависящая от времени BS используется для измерения эффективности калибровки в данный момент времени: \(\textrm{BS}(y)=\frac{1}{n}\sum_{i=1}^n{\left({Z}_i(y)-\hat{S}\left(y| \boldsymbol {x}\right)\right)}^2\). Мы выбрали три временные точки для оценки, а именно 25, 50 и 75% от общего времени наблюдения тестовых данных.

Конкурентные статистические методы

В предложенной нами модели суммирования выживания Лассо Кокс использовался для построения подмоделей на основе путей. Чтобы объединить подмодели, мы использовали solnp (реализованный функцией Rсольп), nLasso/nsslasso (реализовано в пакетеком.ИБахджалам) и ИНС (реализованная с использованием библиотеки TensorFlow (2.3.0) из Python (3.7), а веса могут быть ограничены неотрицательными значениями с помощью kernel_constraint = Non_neg()) в качестве отдельных обучающихся. См. процесс синтеза ИНС на дополнительных рисунках 2 и 3. В качестве моментов времени мы использовали девять равноотстоящих друг от друга величин для распределения наблюдаемых событий, а именно {0, 0,125, 0,25, 0,375, 0,5, 0,625, 0,75, 0,875, 1}. Мы сравниваем эффективность предлагаемого нами метода с несколькими существующими методами одной модели, включая широко используемую регрессию Лассо Кокса (ком.) [27] И расширения, включающие групповые структуры: Group Lasso (gsslasso) (Бахджалам) [28]вложенная группа «Лассо» (grlasso), вложенная группа cMCP и вложенная группа плавного среза абсолютного отклонения (grSCAD) (grpregOverlap) [29]. Эффективность этих методов оценивалась с использованием смоделированных и реальных данных. Все методы одной модели реализованы с использованием параметров по умолчанию. Все анализы проводились с использованием программного обеспечения R (4.1.3).Процессор Dell T7920 Intel Windows 10 Gold 5117 с частотой 2,00 ГГц.